拓扑学在绳结问题中的应用

一、引言

拓扑学是研究几何图形在连续变形下保持不变性质的数学分支，广泛应用于物理学、生物学、计算机科学等领域。其中，绳结问题是拓扑学的重要研究课题，主要探讨如何判断和分类绳结形态，并研究绳结在变形过程中保持不变的特征。

2024 年八省联考数学试题中的扭结问题涉及一条绳子首尾相连后缠绕形成的几何形态，恰好体现了拓扑学在日常问题中的应用。

本文以该问题为例，探讨拓扑学在绳结问题中的基本理论、解决方法及其实际应用。

二、八省联考扭结问题解决

2.1题目

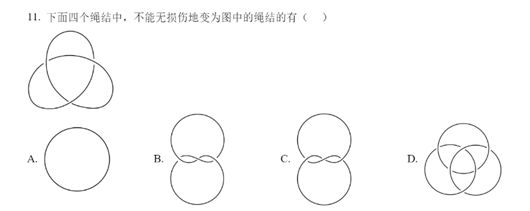
2.2直观解答

下面参考了知乎上的一篇回答。

首先可以选择D选项，因为所给出的三叶结是一根绳子绕成的，而D选项却由三根相互独立的绳子，故必然无法不经过破坏形成，符合题意。

关于A选项，考虑将圆凑成形如图中的形式，可以先把圆扭成一个8字形，假设是右上覆盖右下，只需要从圆形右下方开始向左翻折即可。在形成8字形后尝试把下面的圈以图示方式套到上面去就可形成类似于图中三叶结的样子，而此时会发现，除了最下面的结和左上方的结可以和图示三叶结形成对应以外，右上方的结确实无法对应，因此A也无法通过不破坏的方式形成，符合题意。

对于B选项，考虑将其朝后向上翻折，此时会使得最左边的节点消失并转移到上方，仍然是右下覆盖右上的方式，旋转一定角度和图示形象符合可发现刚好和图示呈镜像对称关系，由上面结论可得其也无法通过不破坏的情况下完成互换，故而符合题意。

由相同的方式对C选项，会使得最右段的节点消失并以右上覆盖右下的方式形成节点，可以看出其和图示三叶结是等价的，故而不满足题意。

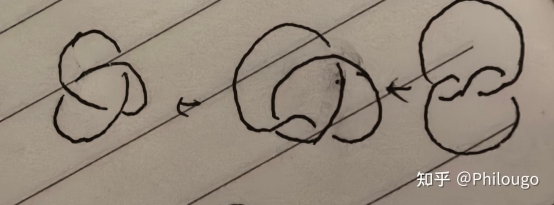
2.3正规解答

2.3.1绳结问题的基本概念

首先给出绳结问题的基本概念：

1. 扭结的数学定义:

绳结在数学上被定义为一个封闭曲线，即在三维空间中首尾相连的光滑曲线。若两条绳结可以通过连续变形（如拉伸、扭转或缩小）互相转换，则称它们为同胚或等价结。

2. 基本类型的绳结：

常见的绳结包括

1)        平凡结：可以通过连续变形拉直成圆环的简单闭合曲线。

2)        三叶结：最简单的非平凡结，呈三角形状。

3)        图解结：由八字形曲线构成的复杂结。

3. 交点数与绳结分类

判断绳结类型的一个常用指标是交点数，即绳结平面投影中绳子交叉的最小次数。交点数可以帮助区分不同类型的绳结。例如，平凡结的交点数为 0，三叶结的交点数为 3，图解结的交点数为 4。

因此我们可以判断出，题目中的A是平凡结，B、C是三叶结。

4. 拓扑不变量在绳结问题中的应用

为了进一步判断绳结的等价性，拓扑学引入了拓扑不变量，即在绳结连续变形过程中保持不变的量。

1)        Reidemeister 移动

Reidemeister 移动是绳结图像变形的三种基本操作，包括：

第一类移动：增加或减少一个环形缠绕。

第二类移动：增加或减少两个相邻交点。

第三类移动：调整交点位置但不改变交点数。

2)        亚历山大多项式

亚历山大多项式是一种通过代数方法描述绳结特征的拓扑不变量。对于任意绳结，亚历山大多项式 满足特定递推关系，并且在同胚绳结间保持不变。

3)        交错数

交错数表示绳结图像中交点的方向性总数。交错数能够区分某些特殊类型的绳结，但无法区分所有绳结。

2.3.2具体问题解决

纽结最基本的特征就是交叉点的数量，交叉数不超过3的只有平凡结，左、右手三叶结。

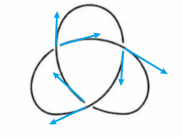
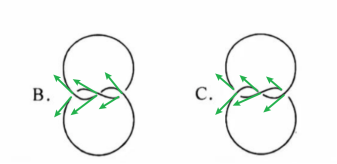
至于如何分辨左右手三叶结，需要了解交叉点的符号：右手三叶结的三个交叉点符号是 （+1，+1，+1），而左手三叶结的三个交叉点符号是 （-1，-1，-1）。

纽结的规范投影图总是会两次经过同一个交叉点，两次经过的方向可能会不同，总共分为两种情况：

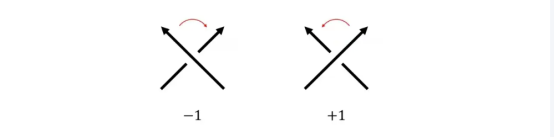
如果从上方翻越过的箭头——上行线，绕交又点顺时针旋转，与下方钻过的箭头——下行线，两者重合，则该交又点记为-1；反之，则记为+1。我们习惯称+1类型的交又点为右手定向的，反之则称为左手定向。这样称呼的原因是将右手拇指与+1类型交又点的粗箭头重合，指向平行；大拇指垂直于纸面向纸外，此时四指自然回握，划过细箭头，且两者方向一致。

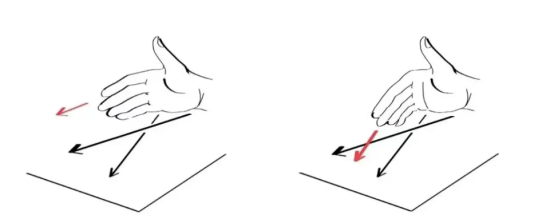
那么现在让我们来试一下题干的图与B、C的区别，发现题干和C的右手拇指方向相同。因此，C能够通过不破坏的方式形成。

三、总结

绳结问题是拓扑学的重要研究课题，通过拓扑变形和不变量分析，可以有效判断绳结的类型及其等价性。

通过学习拓扑学在绳结问题中的应用，我对拓扑学的基本概念和研究方法有了更直观的理解。拓扑学关注图形中点与线的连接关系，强调几何形态在连续变形下保持不变的性质，这种思维方式突破了传统几何对距离和角度的限制，展现了数学研究中更加抽象和广泛的应用领域。