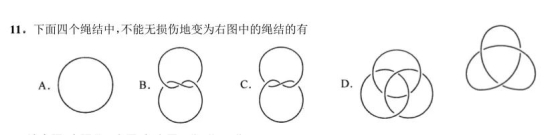
拓扑学在绳结问题中的应用

一、研究背景

拓扑学是研究空间形状、结构和空间在变换下不变性质的数学分支。与几何学不同，拓扑学关注的不是物体的精确形状或尺寸，而是物体的连通性和形状的拓扑不变性。拓扑学广泛应用于多个领域，其中之一就是绳结问题。绳结问题研究的是如何对不同的绳结进行分类以及如何判断两个绳结是否可以通过拉伸、扭曲等变换互相转换。拓扑学的核心概念之一就是拓扑不变量，它能够帮助我们区分不同的绳结，进而解决绳结的分类与判定问题。

二、绳结问题的拓扑学解释

绳结问题主要涉及判断一个绳结是否可以通过某些变形（如拉伸、扭曲、旋转）变为另一个绳结。这里的关键在于“拓扑不变性”——一个绳结的基本结构在变形过程中不会发生变化。拓扑学中的一些重要概念，如同伦、不变量、同胚等，能够有效地帮助我们判断两个绳结是否相同。

三、纽结理论的角度分析

纽结理论（Knot Theory）是拓扑学的一个分支，专门研究在三维空间中闭合曲线的不同类型、如何将它们区分开，以及如何判断一个纽结是否可以通过平滑变形（拉伸、扭曲等）转换为另一个纽结。具体来说，纽结理论提供了以下几方面的分析工具：

1.纽结的分类与同伦变换：纽结理论提供了一套理论工具来判断和分类不同的绳结。通过同伦变换（即在不撕裂或粘连的情况下变换图形的形态），我们可以判断两个绳结是否属于同一类。对于一个复杂的绳结，拓扑学允许我们忽略其具体的形状和尺寸，仅关注其连通性与结构。

2.纽结的不变量：拓扑学中的不变量是解决绳结问题的关键。常见的不变量如绳结的交叉数、结构的类型等。通过这些不变量，拓扑学能够有效地区分不同类型的绳结。例如，若两个绳结具有不同的交叉数，则它们不可能是同一个绳结。其他不变量还包括纽结多项式、Alexander-Briggs多项式、Jones多项式等，这些工具帮助我们更精确地对绳结进行分类。

3.同胚变换与纽结的不可解性：纽结的同胚变换理论表明，如果两个绳结通过拉伸、旋转等操作能够互相转化且不发生断裂或粘连，则它们是同一个纽结。若两个绳结的形状和交叉数不同，它们就无法通过同胚变换互相转化，进而可以被判定为不同的纽结。此外，纽结理论还研究了不可解纽结，即那些无法通过任何平滑变形变为简单圆形的绳结。

四、问题分析与解决

事实上纽结和链环可以在空间中连续变形 , 但不允许剪断和粘合 , 如果一个纽结或链环在经过上述变换后能变成另一个纽结或链环 , 那么我们就称这两个纽结或这两个链环是等价的 , 我们将其定义为同痕 ：

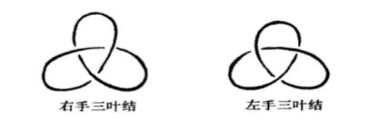
纽结中最基本的特点便是交叉点的个数 , 在数学上交叉点个数不超过 的只有平凡纽结 , 左手三叶结和右手三叶结 , 如上图所示 . 何为三叶结 , 就是旋转 的倍数角度后仍能和自身重合的纽结 . 接下来的任务就是如何区分左手三叶结和右手三叶结 , 故我们需要给出交叉点的定向的定义 , 如下图所示：

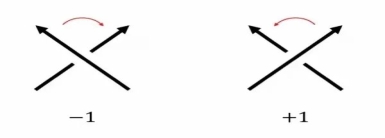
交叉点一共存在两种定向 , 如果从上方翻过去过箭头(上行线)绕交叉点顺时针旋转后与从下方钻过去的箭头(下行线)能重合 , 那么该交叉点记为 , 反之如果从上方翻过去过箭头(上行线)绕交叉点逆时针旋转后与从下方钻过去的箭头(下行线)能重合 , 那么该交叉点记为 , 因此用这个方法可以看到右手三叶结的三个交叉点的符号是 , 而左手三叶结的三个交叉点的符号是 , 进而可以说明左右手三叶结不是同痕的 , 当然要严格区分左右手三叶结还得借助 Jones 纽结多项式：

由于题目所给的是左手三叶结 , 而选项中只有 C 选项是左手三叶结的另一种样貌(我们可以用交叉点的定向作出判断) , B 选项是右手三叶结的另一种样貌 , A 是平凡纽结 , D 是具有三个分支的链环 ，故答案为ABD