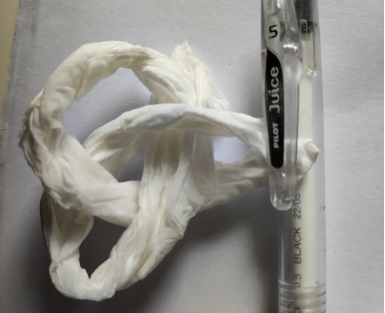
拓扑学在纽结问题中的应用

一．     研究背景

拓扑学关注的是几何图形里点线的连接方式，研究对象是拓扑空间在拓扑变换下的拓扑不变性和拓扑不变量。

以下是教育部命题《2025年高考综合改革适应性演练数学（新八省联考）》第11题绳结问题。

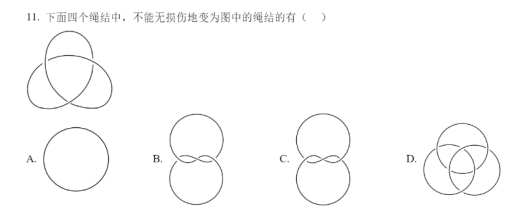
由该题为基础，初步研究有关拓扑学的理论。

二．     研究内容

    该题的答案是ABD。

首先，在考试中遇到这种题目，A为一个环，D为三个环，显然不能无损伤地变为图中的绳结，而BC可以动手操作一下（如鞋带，头发等）。

接下来，进一步理论研究该纽结理论。

在讨论纽结理论之前，我们可以知道生活中的活结和死结本质上只是系得紧不紧，而只要两端都是自由的，本质上都是可以解开的。所以在数学中，纽结理论只研究闭合的绳结。

在纽结理论中，本题A选项被称作unknot（平凡的结），题干中的结就是最简单的unknot，被称作trefoil（三叶结），而题干中提到的将两个绳结进行无损伤地相互转化，被称作等价的结，在拓扑中称为isotopy（同痕）。

对于A选项与题干是否同痕，数学家通过寻找不变量，证明了tricolorability（可三染色性）在三种reidmeister操作下性质不变。由此证明可三染色性是一个在同痕变换下的不变量，并由此推得三叶结与平凡结不等价。但可三染色性仅仅将纽结分为两类，无法解决更为复杂的纽结，于是数学家给出了p染色性（p-colorability），其中p是不为2的质数，依次进行推广，但以上的办法均无法区分B、C选项中两个对称的纽结。实际上，B、C实际上是两种三叶结，分别为左手三叶结和右手三叶结，并称作手性。在1984年，数学家Jones发现了一种新的不变量，现在被称为Jones多项式（琼斯多项式），并在1990年获得菲尔兹奖。我们可以算出C选项的Jones多项式为，而B选项的Jones多项式为，由此得出B与题干中的纽结不等价，因此不能由同痕变换得到。

当然在考场中，还是鞋带更为简便。

三．     该题的其他解法

以下解法从B站看到。

1.解法一

2.解法二

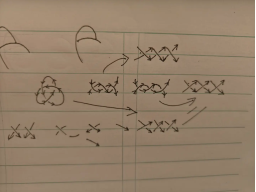
3.解法三

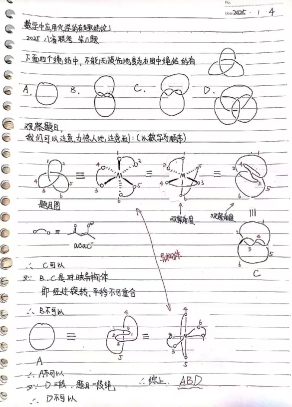
4.解法四