判别可数集与不可数集

数学jd1601班  王安冬小组

一、       背景：

1.1  历史背景

集合论是德国著名数学家Cantor于19世纪末创立的。十七世纪，数学中出现了一门新的分支：微积分。在之后的一二百年中这一崭新学科获得了飞速发展并结出了丰硕成果。其推进速度之快使人来不及检查和巩固它的理论基础。十九世纪初，许多迫切问题得到解决后，出现了一场重建数学基础的运动。正是在这场运动中，Cantor开始探讨了前人从未碰过的实数点集，这是集合论研究的开端。到1874年Cantor开始一般地提出“集合”的概念。他对集合所下的定义是：把若干确定的有区别的（不论是具体的或抽象的）事物合并起来，看作一个整体，就称为一个集合，其中各事物称为该集合的元素。

随着集合论的不断发展，其各项内容也逐渐得到完善。Cantor通过一一对应关系建立了集合之间对等的概念，奠定了无限集分类的基础；引进了可数集的概念，证明了有理数全体集代数数（有理多项式的根）全体都是可数集；运用对角线方法证明了实数集是不可数集等等。如今，可数集与不可数集仍是研究集合的基础，在实变函数、拓扑学、离散数学中都是很重要的基础。

1.2  发展方向

目前，可数集与不可数集的研究仍然在进行之中，如下列几篇文章，均是在可数集以及不可数集的基础上进行研究：

二、 可数集与不可数集

2.1 定义

设 A 和 B 是两个集合，讨论集合中元素的多少问题，如果 A 和 B 都是有限集，则只需分别数出它们的元素个数，再加以比较即可；但是当 A 和 B都是无限集时，无法数出它们的元素个数，此时可通过“映射”的概念建立集合间的等势关系，并拓广集合中元素个数的概念，引进集合基数的概念，最后将集合分为可数集和不可数集。

可数集：可数集是指能与自然数集N建立一一对应的集合，又称可列集。如果将可数集的每个元素标上与它对应的那个自然数记号，那么可数集的元素就可以按自然数的顺序排成一个无穷序列a1，a2，a3，…,an，…

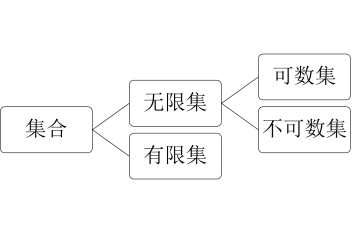
不可数集：不可数集是既不是有限集合，也不是（无限）可数集的集合。

2.2 性质

由于可数集与不可数集在无限集里面具有对偶关系，而研究其性质对于区分可数集和不可数集有很好的帮助。下面介绍可数集的相关性质：

2.3 实例

1.常见可数集：

自然数集

非负偶数集

非负奇数集

整数集

有理数集

2.常见不可数集：

实数集 R

无理数集 R\Q

区间 [0,1]

Cantor集

三、 不可数集判断

3.1 构造映射

首先介绍对等的概念：如果两个集合之间能够建立元素间一一对应的关系，即集合A、B之间存在一一映射，则称两个集合对等，记作A~B，并称集合A、B的基数相同，记作card A=card B。

对于一个集合，若需要判断它是否为不可数集，可以尝试是否能将该集合与已知的不可数集之间构造一一映射关系，若可以，则判断该集合为不可数集。

例：判断(0,1)是否为不可数集。

证：区间(0,1)是不可数集

已知，区间[0,1]为不可数集，尝试构造区间(0,1)与区间[0,1]之间的一一映射。

在[0,1]中可以取，

在(0,1)中可以取，

故构造映射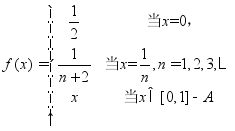

则是区间(0,1)与区间[0,1]之间的一一映射，所以区间(0,1)与区间[0,1]对等，所以区间(0,1)为不可数集。

3.2 应用定义判断

根据不可数集的定义，在无限集合中，不是可数集的集合即为不可数集，而可数集是指能与自然数集N建立一一对应的集合，又称可列集。由于不可数集的定义实依托于可数集而定义的，故在判断集合是否为不可数集时，可以应用定义判断它不是可数集，即应用反证法。

例：判断(0,1)是否为不可数集。

证：区间(0,1)是不可数集。

假设区间(0,1)是可数集，则区间(0,1)可以表示为；

用十进制小数表示为：        

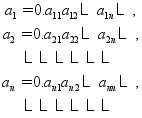
记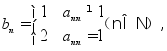

则对

这与矛盾，故假设不成立，所以区间(0,1)是不可数集。

3.3 子集不可数

根据可数集的性质，可数集的子集之多是可数的，即可数集的子集可能是空集，可能是有限集，可能是无限集中的不可数集。对偶到不可数集，不可数集的子集至多是不可数的，即不可数集的子集可能是空集，可能是有限集，可能是无线集中的可数集，也可能是无线集中的不可数集。换言之，我们在判断一个集合不可数时，可以通过寻找改集合是否存在不可数子集来进行判断。

例：判断笛卡尔积是否为不可数集。

证：笛卡尔积是不可数集。

选取笛卡尔积的一个子集进行研究，令，显然；

构造不可数集R与集合A之间的一一映射f，

可以令

显然f是不可数集R与集合A之间的一一映射，所以集合A也是不可数集。

因为笛卡尔积为无限集，其存在一个不可数子集A，而可数集的子集至多为可数集，不可数集的子集至多为不可数集，所以笛卡尔积是不可数集。

四、 不可数集应用

随着数学的研究不断发展应用，集合论作为数学的重要分支也展现了强大的活力，可数集与不可数集的研究也不断向前。

五、 总结

集合作为各项数学分支研究的基础，在拓扑学中通过集合引申出关系、映射、度量空间以及拓扑空间等等；在离散数学中则通过集合引申出关系、映射、群、半群、环等等；而在基础数学中，包括函数等等都是在集合的基础上进行研究的，可见集合作为学习基础的重要性。同时，可数与不可数是集合的重要特点，通过集合可以拓展到空间，具有重要研究意义。

如何判别集合的不可数性质，本小组通过查阅相关资料，总结主要有三种方法进行判别，希望能够通过分享给予同学们一些帮助，同时也希望可以和大家一同交流。若本文中存在些许错误，希望大家见谅。

学习小组

组长：王安冬

组员：杨铭、胡琪昕、智静怡、徐婧文

                                                                2019年3月10日