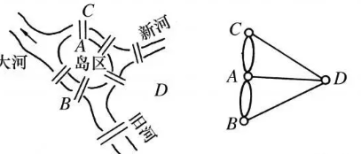
拓扑学简介：

点集拓扑学产生于19世纪。G.康托尔建立了集合论，定义了欧几里得空间中的开集、闭集、导集等概念，获得了欧几里得空间拓扑结构的重要结果。1906年M.-R.弗雷歇把康托尔的集合论与函数空间的研究统一起来，建立了广义分析，可看为拓扑空间理论建立的开始。F.豪斯多夫在《集论大纲》（1914）中用开邻域定义了比较一般的拓扑空间，标志着用公理化方法研究连续性的一般拓扑学的产生。随后波兰学派和苏联学派对拓扑空间的基本性质（分离性、紧性、连通性等）做了系统的研究。经过20世纪30年代中期起布尔巴基学派的补充（一致性空间、仿紧性等）和整理，一般拓扑学趋于成熟，成为第二次世界大战后数学研究的共同基础。

拓扑学是把那些很朴素但又很基本的图形的集和直观性质，进行数学化的结果。在漫长的历史过程中，人们用很多种数学方法来表达这种几何图形的直观性质，直到康托提出了集合论之后，以集合论为基础，配之以映射概念，拓扑学有了根本性的发展。从欧拉的七桥问题，地图着色问题，Jordan曲线定理等知道平面上简单闭曲线将平面分成两部分。高斯研究扭结和二重积分的联系等是当时研究的一些孤立问题，而后成为拓扑学的有关问题。再到黎曼发现了多值函数解析函数可转化为闭曲面上的单值函数，并得出闭曲面的拓扑分类。拓扑学都有着很深刻的发展。

拓扑学应用：

1、机械性能在固体中的拓扑依赖性在机械工程和材料科学学科中。电气和机械性能取决于材料中分子和基本单元的布置和网络结构。研究了皱褶拓扑的抗压强度，试图了解这种主要是空白空间的结构的高强度重量。拓扑在接触力学中具有重要意义，其中刚度和摩擦对表面结构的维数的依赖性是多体物理学中应用的关注点。

2、拓扑量子场理论（或拓扑场理论或TQFT）是计算拓扑不变量的量子场理论。

3、Calabi-Yau歧管的拓扑分类在弦理论中具有重要的意义，因为不同的歧管可以承受不同种类的弦。

4、在宇宙学中，拓扑可用于描述宇宙的整体形状。这个区域被称为时空拓扑。

5、机器人的各种可能的位置可以由称为配置空间的歧管来描述。在运动规划领域，可以在配置空间中找到两点之间的路径。这些路径表示机器人的关节和其他部分进入所需位置和姿势的运动。

生活中的较为简单的拓扑学：

在拓扑学上，甜甜圈和咖啡杯本质上相同，球体和立方体本质上相同：

魔术结：

莫比乌斯环：

七桥问题：