从“七桥问题”谈拓扑学

数学jd2001杨继来

七桥问题是一个著名的数学问题，它可以被看作是拓扑学的开端之一。拓扑学是数学的一个分支，研究的是几何图形的形变和不变性质。在拓扑学中，我们关注的是空间形态的变化，而不关心其大小和角度。因此，拓扑学家通常把一个形状看作是由一些连通的区域和它们之间的连接关系所构成的。例如，一个球体可以看作是一个连续的曲面，而一个圆环则可以看作是一个带有一个环状孔洞的面片。

拓扑学中的一个重要概念是拓扑等价，也就是说，如果两个空间形态可以通过连续的变形相互转换，那么它们就是拓扑等价的。例如，一个球体和一个橡皮球可以通过不断地拉伸和压缩橡皮球的表面而相互转换，因此它们是拓扑等价的。拓扑等价关系可以用于定义拓扑空间的分类。

七桥问题是著名的数学问题，最早由欧拉在18世纪提出。问题的描述如下：有一座连接着两岸的岛屿，这座岛屿上有7座桥，游客们想要游览整座岛屿上的所有地方，但是每座桥只能经过一次。问题是能否设计一条行走路线，使得游客能够走遍整座岛屿上的所有地方。

我们可以用图论的语言来描述这个问题。将岛屿上的每个地方看做一个节点，将每座桥看做一条边。那么我们得到的就是一个无向图。在这个图中，节点的度数是指与这个节点相邻的边的数目。例如，岛屿的中心点有4条边与之相邻，因此它的度数为4。

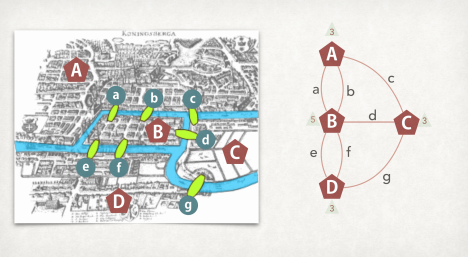欧拉通过对这个无向图的度数进行分析，证明了这个问题的无解性。具体地说，如果一个无向图中恰好有两个节点的度数是奇数，那么这个图就不能构成欧拉通路，也就是说，不能设计一条行走路线使得每条边都被恰好经过一次。在七桥问题中，岛屿上恰好有两个节点的度数是奇数，因此这个问题是无解的。

七桥问题虽然看起来很简单，但它引发了人们对拓扑学的深入研究。拓扑学的一个重要应用是在物理学中。拓扑材料是一种新型的材料，它们具有特殊的电子结构和拓扑不变量，可以在某些条件下表现出特殊的电子输运性质。拓扑绝缘体是一种典型的拓扑材料，它在内部是绝缘体，但在表面却可以传导电子。这种材料具有重要的电子学和量子计算的应用价值。

拓扑学也有广泛的应用在计算机科学中。在计算机科学中，拓扑学可以用于设计和分析网络拓扑结构，例如，在无线传感器网络中，设计一种合理的拓扑结构可以提高网络的通信质量和能耗效率。

此外，拓扑学还有应用在图像处理、信号处理、语言处理和社交网络等领域中。例如，在社交网络中，拓扑学可以用于分析社交网络中节点的联系和社群的结构，从而更好地理解社交网络的特征和演化规律。

七桥问题是拓扑学的开端之一，它揭示了拓扑学中的一个重要概念——拓扑等价，并引发了人们对于拓扑学的深入研究。在拓扑学中，我们研究的是几何形状和空间结构之间的关系，而不考虑其具体的度量或坐标。这种无度量的研究方式使得拓扑学在不同领域中都有广泛的应用。

除了在物理学、计算机科学、图像处理、信号处理、语言处理、社交网络等领域中的应用外，拓扑学还有许多其他的应用。例如，在化学中，拓扑学可以用于分析分子的结构和化学键的性质，从而帮助我们更好地理解分子的性质和化学反应的机理。在生物学中，拓扑学可以用于分析蛋白质和DNA的结构和功能，从而帮助我们更好地理解生物分子的性质和生物过程的机理。

总之，七桥问题是拓扑学的开端之一，它为我们理解拓扑学的重要概念——拓扑等价提供了一个简单而又具体的例子。拓扑学的应用已经渗透到许多领域，它不仅有助于我们更好地理解自然界和社会现象中的结构和性质，也有助于我们设计更加高效和优化的系统和技术。