第6章-知识点3 频率响应的对数坐标图

教学目标：使学生掌握典型环节的Bode图和系统Bode图作法。

对数幅频特性坐标：将幅频A(ω)取常用对数后再乘以20，作为纵坐标，用L(ω)表示，按线性分度；横坐标为频率ω，按对数分度。

优点：

a、合理利用纸张；

b、简化乘除运算为加减运算；

c、用渐进线近似曲线，作图方便。

1、典型环节Bode图

1）比例(或放大)环节：G1(s)=K

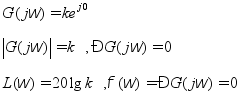
2）(理想)积分环节：G2(s)=1/s

3）(理想)微分环节：G3(s)= s

积分环节频率响应特性: G2(jω)=1/jω

微分环节频率响应特性: G3(jω)= jω

其中：蓝线为一重积分环节曲线

红线为二重积分环节曲线

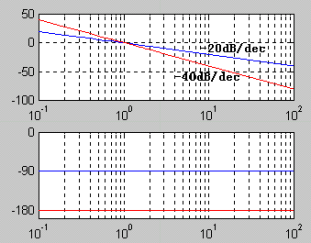
4）(一阶)惯性环节： G4(s)=1/(T s+ 1)

5）一阶微分环节：  G5(s)=τs + 1

惯性环节频率响应特性:   G4(jω)= 1/(T jω + 1)

一阶微分环节频率响应特性: G5(jω)=τjω + 1

其中：红色曲线为精确曲线, 蓝色曲线为近似曲线, 横坐标单位为1/T rad/s

6）(二阶)振荡环节：

7） 二阶微分环节：

二阶振荡环节频率特性:  G6(jω)= 1/[(1- T2ω2 )+2ζTωj ]

二阶微分环节频率特性:  G7(jω)= (1-τ2ω2) + 2ξτωj

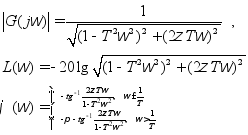
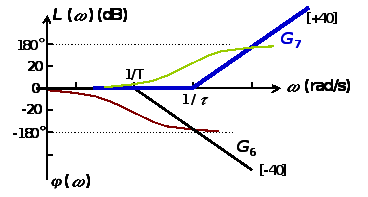
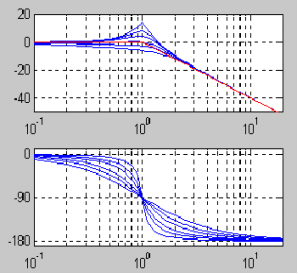
其中：红色曲线为近似曲线，蓝色曲线依次是当参数为0.1，0.2，0.3，0.5，0.7，1.0时的精确曲线。横坐标单位为1/T （rad/s）。

2、两个性质

性质1：

性质2：

[例1]：有闭环系统：

其中：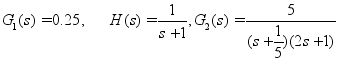

作系统开环对数幅相频特性曲线。

[例2]：设系统的开环传递函数为：

试绘制系统的开环对数频率特性曲线和开环幅相特性曲线。

解： ①绘制开环对数频率特性曲线：

且：

②开环幅相特性曲线：

[例3]：设系统的开环传递函数为：，试绘制系统的开环对数频率特性曲线和开环幅相特性曲线。

解： ①绘制开环幅相特性曲线：

②开环对数频率特性曲线：

[例4]:

该系统可认为由五个典型环节组成:

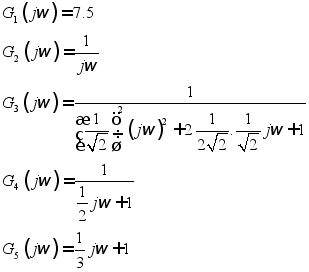
图中:蓝色曲线为各环节的近似曲线，绿色曲线为各环节的精确曲线，红色曲线为总的近似曲线，黄色曲线为的总的精确曲线。

3、最小相位系统

如果系统的传递函数在S右半平面既无极点，又无零点，则称之为最小相位系统。对于最小相位系统，知道幅频特性，其相频特性就唯一确定，所以只需画它的幅频特性就可以了。

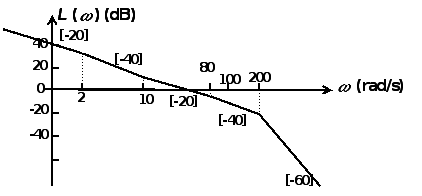
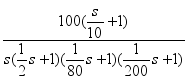
         时间常数确定:

由伯德图的作图过程可知幅频曲线的转折点对应的频率是时间常数的倒数, 且当曲线斜率增加时对应的是一阶微分环节的时间常数,当曲线斜率减少时对应的是一阶惯性环节的时间常数.