第2章-知识点4 典型环节及其传递函数

教学目的：使学生掌握典型环节的概念；熟悉常用元部件的传递函数，明确系统常用的传递函数形式。

基本环节：基本方式和动态性能相同的环节。任何复杂的控制系统都是由最基本的典型环节所组成的。

1、控制系统典型环节

（1）比例环节:  输出随输入成比例变化

其传递函数为：

①弹性元件：位移随外力大小成比例变化，比例系数取决于元件的弹性大小，与输入输出无关。

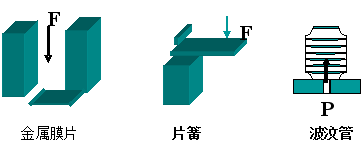
位移在弹性范围内遵循虎克定律：

传递函数为：

②节流元件：前后压力差的大小随气流量成比例变化，比例系数取决于元件的气阻大小，与输入输出无关。

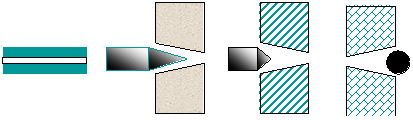
传递函数为：

③喷嘴挡板机构：输出压力随喷嘴挡板的开度成比例变化

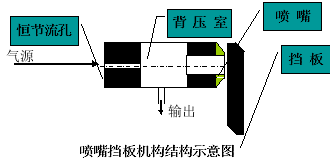
④运算放大器

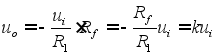
（2）积分环节: 输出与输入对时间的积分成比例。

微分方程：

传递函数：

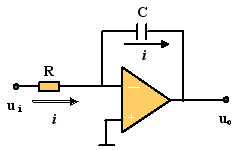例1.R-C积分电路

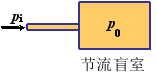
例2．气容

Δm--是空气储存量的增量；△p--是气压室压力增量.

气体质量流量

因：      

气容传递函数：

（3）一阶惯性环节(非周期环节)

  输入突变时，输出的变化滞后于输入的变化，并按一定的规律趋近于输入值。 

微分方程式为:

传递函数：

例1.RC电路

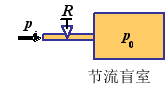
例2.节流盲室组成的一阶惯性环节

微分方程：

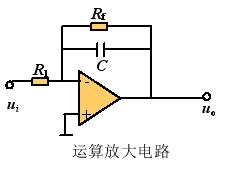传递函数：

例3.运算放大器

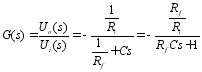
（4）一阶微分环节：输出与输入的微分成比例。

微分方程：

传递函数：

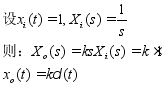    因此，理想的微分环节在实际中并不存在。

实际的微分环节：理想的微分环节与惯性环节的串联。

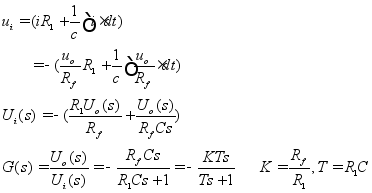
一阶微分：

（5）振荡环节(含有两种形式的储能元件)

微分方程：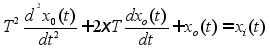

传递函数为:

例1：RLC电网络

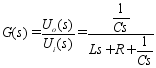
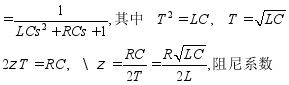
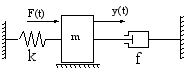例2.质量－弹簧－阻尼器系统

（6）恒时延环节

输入xi(t)与输出xo(t)之间有：

其传递函数：

1)、测量元件离被控对象有一段距离；

2)、物料传输过程中，因距离远而产生时延。

2.对传递函数的几点说明

①、传递函数只适用于线性系统，而不适用于非线性系统。因为传递函数是在拉氏变换的基础上导出的，而拉氏变换是一种线性积分变换，只适用于线性微分方程，非线性系统不能用线性微分方程来描述，也就不能用传递函数表示。

②、传递函数中的各项系数与微分方程中的各项系数对应相等，完全由系统的内部结构、参数决定，而与输入量的大小和形式无关，故传递函数与微分方程一样，均可作为系统的动态数学模型。

③、传递函数的结构形式及参数虽然相同，但输入、输出的物理量不同，则代表的物理意义不同。从另一方面说，两个完全不同的系统（例如一个是机械系统，一个是电子系统），只要它们的控制性能一样，就可以有完全相同的传递函数。这就是在实验室做模拟实验的理论基础。

④、G(s)的拉氏逆变换是系统的脉冲响应：

⑤、传递函数只表明线性系统的零状态响应特性，它是由系统工作状态相对静止时得出的。这时可认为，对于相对给定的平衡点，系统输出量和输入量的初始值均为零，这才符合传递函数的定义。

⑥、传递函数分子多项式的阶次总是低于至多等于分母多项式的阶次，即 m≤n 。这是因为实际物理系统或元件中总是含有较多的惯性元件，以及能源又是有限的缘故。传递函数分母中S 的最高阶次等于输出量导数的最高阶次。如果s 的最高阶次为n ，则系统称为n 阶系统。

⑦、传递函数的三种常用表示形式：